Greedy Algorithm Optimization Proof

2021 A crystal symmetry-invariant KobayashiWarrenCarter grain boundary model and its implementation using. Consider edges in ascending order of cost.

Cs333 Cutler Greedy1 Introduction To Greedy Algorithms The Greedy Technique Problems Explored The Coin Changing Problem Activity Selection Ppt Download

NEAT stands for NeuroEvolution of Augmenting Topologies.

Greedy algorithm optimization proof. Let some constant k. It begins by considering an arbitrary solution which may assume to be an optimal solution. The proofs structure is worth noting because it is common to many correctness proofs for greedy algorithms.

Both greedy algorithms compute. NEAT implements the idea that it is most effective to start evolution with small simple networks and allow them to become increasingly complex over generations. In many problems a greedy strategy does not produce an optimal solution but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.

The greedy algorithm first appeared in the combinatorial optimization literature in a 1971 article by Edmonds 62 though the theory of matroids dates back to a 1935 article by Whitney 200. In probability theory and machine learning the multi-armed bandit problem sometimes called the K-or N-armed bandit problem is a problem in which a fixed limited set of resources must be allocated between competing alternative choices in a way that maximizes their expected gain when each choices properties are only partially known at the time of allocation and may. The Clique Decision Problem belongs to NP-Hard A problem L belongs to NP-Hard if every NP problem is reducible to L in polynomial timeNow let the Clique Decision Problem by C.

C Can the time complexity of above function be reduced. This algorithm is based on the principle of optimism in the face of uncertainty. Distribution of action-value functions for 3 different arms a1 a2 and a3 after several trials is shown in the figure above.

Proof of Correctness Part 2 Undirected Connectivity. But in fact the greedy algorithm does work and yields the best- t subspaces of every dimension as we will show. In the above code funn is equal to 2funn-1.

Of course Im taking this a bit too far by adding the same script 100 times but this is just a proof of concept. Let GV E be a connected weighted graph and let T be. 2020 Optimization framework and clustering-based algorithm for energy-aware adaptive sensing.

Approaches to analyzing lower bounds on problems and upper bounds on algorithms. CONNECTIVITY IN DIRECTED GRAPHS 1202011. Same greedy strategy to nd the best three and higher dimensional subspaces de nes v 3v 4in a similar manner.

For jointly constructing a random graph from a given degree sequence and its exploration. Let T be the spanning tree of graph G generated by Prims algorithm and T be the. Classical algorithm design techniques including algorithms for sorting searching and other operations on data structures such as hash tables trees graphs strings and advanced data structures dynamic programming and greedy approaches.

Introduction to Randomized Algorithms 282011. To prove that C is NP-Hard we take an already known NP-Hard problem say S and reduce it to C for a particular instance. The knapsack problem is to find the set of items such that the total weight is less than or equal to a given limit size of knapsack and the total valueprofit earned is as large as possible.

For example for n 3. Consider the following questions for above code ignoring compiler optimization. Second we consider optimality.

Algorithm types such as divide-and-conquer backtracking greedy and dynamic programming are analyzed using mathematical tools such as generating functions recurrence relations induction and recursion graphs and trees and permutations. 2020 Necessary and Sufficient Null Space Condition for Nuclear Norm Minimization in Low-Rank Matrix Recovery. Second it is proved that the constructed spanning tree is of minimal weight.

We prove a large deviation principle for the greedy exploration of configuration models building on a time-discretized version of the method proposed by Bermolen et al. Performance metrics and statistical analysis results clearly revealed that the proposed IMOMRFO is a competitive algorithm for finding PS t the space of decision variables belonging to the optimization problem and PF t the space of objective functions which represent optimum solution sets for multi-objective problems of different types and. The Knapsack Problem is a classic combinatorial optimization problem that has been studied for over a century.

A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. Start with any vertex s and greedily grow a tree T from s. At each step add the cheapest edge to T that has exactly one endpoint in T.

Our proof of the correctness of the greedy algorithm for. So the above function returns 2 n. The convince us that Prims algorithm is correct lets go through the following simple proof.

2021 Improved penalty algorithm for mixed integer PDE constrained optimization problems. Tips on how to minimize Google Tag Managers impact on page speed. First it is proved that the algorithm produces a spanning tree.

The proof consists of two parts. B What is the time complexity of above code. Yao Algorithmica 59 2011 510-520.

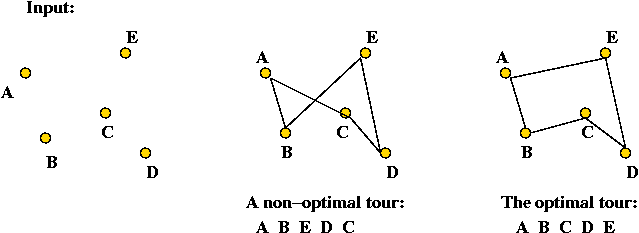
Tight Approximation Ratio of a General Greedy Splitting Algorithm for the Minimum k-Way Cut Problem Mingyu Xiao Leizhen Cai and Andrew C. In other words the more uncertain we are about an arm the more important it becomes to explore that arm. An example of the greedy algorithm for interval scheduling.

In our opening exam- ple of greedy algorithms the activity-selection problem we get to the greedy algorithm more directly than we did in the second edition. It is a method for evolving artificial neural networks with a genetic algorithm. And Brightwell et al.

The PTAS described here is an exhaustive search that employs the previously described greedy algorithm. Correctness of Greedy Algorithm Part 1 Correctness of Greedy Algorithm Part 2 11. Prims algorithm is a Greedy Algorithm because at each step of its main loop it always try to select the next valid edge e with minimal weight that is greedy.

Add the next edge to T unless doing so would create a cycle. The proof of this result follows the general strategy to study large deviations of. A What does the above code do.

The way we delete a node from binary search trees which includes red-black trees now guarantees that the node requested for deletion is the node that is actually deleted. This is captured in the following de nitions. Maybe your container will have fewer tags that manipulate the DOM but their impact will greater due to their complexity.

Space Optimization The Floyd-Warshall Algorithm Part 1 The Floyd-Warshall. Engineering Applications of Artificial Intelligence 95 103841. Fractional Knapsack problem is defined as Given a set of items having some weight and valueprofit associated with it.

What does funn do. Two Greedy Algorithms Kruskals algorithm. The nal schedule is f147g.

The course often includes a section on abstract complexity theory including NP completeness. Algorithm Design Foundations Michael T. There is no apriori guarantee that the greedy algorithm gives the best t.

Computers Mathematics with Applications 30. Graph Coloring Applied to Secure Computation in Non-Abelian Groups Yvo Desmedt Josef Pieprzyk Ron Steinfeld Xiaoming Sun Christophe Tartary Huaxiong.

Greedy Algorithms Bil 741 Advanced Analysis Of Algorithms

Greedy Algorithms Bil 741 Advanced Analysis Of Algorithms

The Foundations Logic And Proofs Chapter 3 Algorithms

Greedy Algorithms Ppt Download

Greedy Algorithms Ppt Download

Epsilon Greedy Policy Improvement Cross Validated

Is Dijkstra S Algorithm A Greedy Algorithm Or A Dynamic Programming Algorithm Quora

Greedy Algorithms Bil 741 Advanced Analysis Of Algorithms

Greedy Algorithms Ppt Download

Greedy Algorithms Bil 741 Advanced Analysis Of Algorithms

Greedy Algorithms Ppt Download

Cs333 Cutler Greedy1 Introduction To Greedy Algorithms The Greedy Technique Problems Explored The Coin Changing Problem Activity Selection Ppt Download

Greedy Algorithm What Is A Greedy Algorithm By Osgood Gunawan Medium

Greedy Algorithms Ppt Download

Ppt Greedy Algorithms Powerpoint Presentation Free Download Id 2511397

Algorithms

Greedy Algorithms Ppt Download

Algorithms For Np Hard Problems Section 20 2 A Greedy Heuristic For Maximum Coverage Part 2 2 Youtube

Cs333 Cutler Greedy1 Introduction To Greedy Algorithms The Greedy Technique Problems Explored The Coin Changing Problem Activity Selection Ppt Download