Algorithm Substitution Method Examples
So the real question is whether induction is justified. Firstly guess a solution for the given equation.

Direct Substitution Method Youtube
First step is to write the above recurrence relation in a characteristic equation form.

Algorithm substitution method examples. Show activity on this post. If peopleiequalsKent return Kent. We have to obtain the asymptotic bound using recursion tree method.
If as in a T n n l g n n you just substitute to get the one you ask To here. 4x 2 x 3 2. Therefore Tn O na bn O na and since Tn is both O na and Ω na.
Use the substitution method to show that. 1 Substitution method Consider a computational problem P and an algorithm that solves P. First we eliminate x 1 from the second equation by subtracting 3 times the rst equation from the second.
We make a guess for the solution and then we use mathematical induction to prove the guess is correct or incorrect. Let Tn be the worst-case time complexity of the algorithm with nbeing the input size. Is O n lg n.
When plain text is encrypted it becomes unreadable and is known as ciphertext. Return. Guess the form of the solution.
Simple Examples of Recursive Algorithms Factorial Finding maximum element of an array Computing sum of elements in array Towers-of-Hanoi Problem Recurrence Equation to Analyze Time Complexity Repeated substitution method of solving recurrence Guess solution and prove it correct by induction. Let us discuss few examples to appreciate how this method works. T n 4Tleft frac n 2 right n T n 4T.
The substituted LHS of the recurrence is kna kbn which is larger than kna 2kbcn as long as kb2kbc or b. 1 Substitution Method. Example Consider the system of linear equations x 1 2x 2 x 3 5.
This naturally gives rise to runtime recurrences which express the algorithm on runtimes of input size n. Tn n if n 1 or n 0 Tn 1 Tn 2 otherwise. S m 2 m S 0 2 m 2 m 2 m 2 m m 2 m 2 m.
Tn Tn2 1 is an example of a recurrence relation A Recurrence Relation is any equation for a function T where T appears on both the left and right sides of the equation. Consider the following recurrence. Suppose we want to solve.
The Fibonacci recurrence relation is given below. Data Structure Analysis of Algorithms Algorithms. If peopleiequalsJohn return John.
A Recursion Tree is best used to generate a good guess which can be verified by the Substitution Method. As they say it is a guess. Subproblem is simply solved in a straightforward manner.
Here we will see how to use substitution method to solve recurrence relations. O n l g n. The substitution method for solving recurrence relations consists of three steps.
In this video I have discussed how to solve a recurrence relation using the substitution method for solving algorithm complexity with the help of an example. T n 4 T n 2 n. We always want to solve these recurrence relation by get-ting an equation for T where T appears on just the left side of the equation 3.
3x 1 2x 2 4x 3 17. S m 1 2 S m 2 2 m 1. For example consider the recurrence Tn 2Tn2 n We guess the solution as Tn OnLogn.
In the example given in the previous chapter T 1 T 1 was the time taken in the initial condition. 4x 1 4x 2 3x 3 26. Replace the body of the method that implements the algorithm with a new algorithm.
Now using mathematical induction prove that the guess is correct. MASTER METHOD In this method we have some predefined recurrence equation cases and our focus is to get a direct solution for it. 4x 1 4x 2 3x 3 26.
We do so by iterating the recurrence until the initial condition is reached. There is no requirement that b be positive so choosing k1 b 1 satisfies the recurrence. Iteration Method for Solving Recurrences.
An example is given below to show the method in detail. In past lectures we have seen two examples of divide and conquer algorithms merge sort and the median-of-medians approach to the selection problem. In a Substitution cipher any character of plain text from the given fixed set of characters is substituted by some other character from the same set depending on a key.
For example with a shift of 1 A would be replaced by B B would become C and so on. We use these steps to solve few recurrence relations starting with the Fibonacci number. Suppose we are using the binary search technique.
T n 2 T n 2 n Tn 2Tleftfrac n2right n T n 2 T 2 n n. We need to prove that Tn. Lets take a look at an example.
In this technique we check whether the element is present at the end or not. Before String foundPersonString people for int i 0. T n 4T n.
In this method we first convert the recurrence into a summation. The Recursion tree for the above recurrence is. Consider T n 2T n 2.
We will take two examples to understand it in better way. For searching and sorting Tn denotes the number of. Now we use induction to prove our guess.
I if peopleiequalsDon return Don. This yields the equivalent system x 1 2x 2 x 3 5.

Gate Ese Back Substitution Method For Solving Recurrences Offered By Unacademy

Substitution Method For Solving Recurrences With Example Programmerbay

Back Substitution Examples Youtube

Algorithm 1 Growth Of Functions And Solving Recurrences By Temp Jun Devpblog Medium

Gate Ese Back Substitution Method For Solving Recurrences Offered By Unacademy

Substitution Cipher Geeksforgeeks

Substitution Method For Solving Recurrences With Example Programmerbay

Substitution Method For Solving Recurrences With Example Programmerbay
Substitution Method Review Systems Of Equations Article Khan Academy
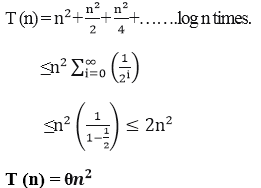
Daa Recursion Tree Method Javatpoint

Backward Substitution An Overview Sciencedirect Topics

Substitution Method Definition Steps Examples

Recurrence Relation Iteration Method Youtube

Solving Recurrence With Substitution Method Mathematics Stack Exchange
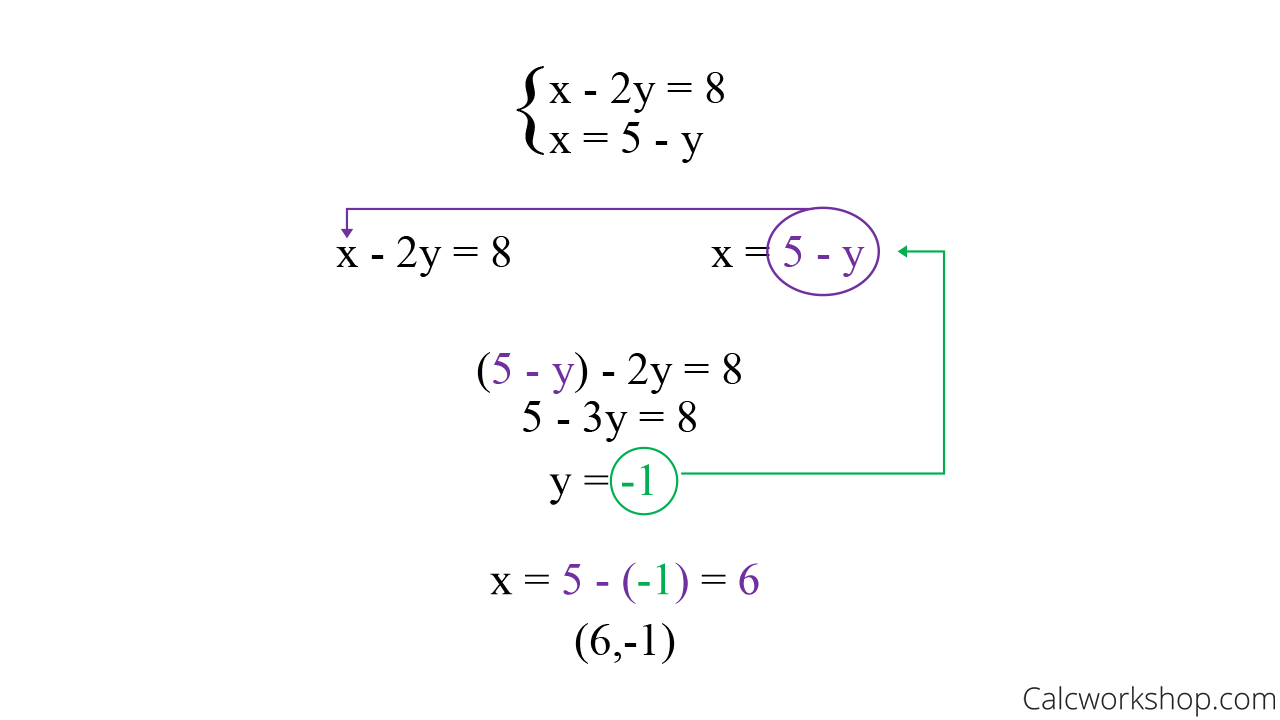
What Is The Substitution Method Just 3 Simple Steps

Algebraic Elimination Method Class 10 Ncert Solutions Suresolv

Explanation Of Backwards Substitution In Gaussian Elimination Mathematics Stack Exchange

Solving Recurrences With The Substitution Method Mathematics Stack Exchange

Substitution Method For Solving Recurrences With Example Programmerbay
Komentar
Posting Komentar